El concepto de incertidumbre como un atributo cuantificable es relativamente nuevo en la historia de las mediciones, a pesar de que los conceptos de error y análisis del error han sido parte de la práctica de la ciencia de la medición por largo tiempo.

La incertidumbre nos da una indicación de la calidad del resultado, de manera tal que el usuario puede apreciar su confiabilidad y de este modo se pueden comparar sus resultados contra alguna especificación o norma.

En la sección 2 de la Guía para la estimación de la incertidumbre en la medición (GUM) JCGM 100: 2008 se define el concepto de incertidumbre de medida.

Los análisis de incertidumbre suelen ser difíciles para la mayoría, extienden nuestra comprensión de la medición hasta el límite, y cuanto menor sea la incertidumbre requerida en una medición, mayor será la comprensión requerida. Es una de las razones para enfatizar los análisis de incertidumbre en los entornos de calibración y prueba, especialmente donde se desea obtener la acreditación del laboratorio.

Fuentes de incertidumbre

«La incertidumbre del resultado de una medición refleja la imposibilidad de conocer exactamente el valor del mensurando»

Guía para la estimación de la incertidumbre en la medición (GUM), JCGM 100: 2008.

El resultado de una medición tras la corrección de los efectos sistemáticos identificados es aún una estimación del valor del mensurando.

En la práctica existen numerosas fuentes posibles de incertidumbre en una medición, entre ellas:
a) Definición incompleta del mensurando.
b) Realización imperfecta de la definición del mensurando.
c) Muestra no representativa del mensurando, la muestra analizada puede no representar al mensurando definido.
d) Conocimiento incompleto de los efectos de las condiciones ambientales sobre la medición, o medición imperfecta de dichas condiciones ambientales.
e) Lectura sesgada de instrumentos analógicos, por parte del técnico.
f) Resolución finita del instrumento de medida o umbral de discriminación.
g) Valores inexactos de los patrones de medida o de los materiales de referencia.
h) Valores inexactos de constantes y otros parámetros tomados de fuentes externas y utilizados en el algoritmo de tratamiento de los datos.
i) Aproximaciones e hipótesis establecidas en el método y en el procedimiento de medida.
j) Variaciones en las observaciones repetidas del mensurando, en condiciones aparentemente idénticas.

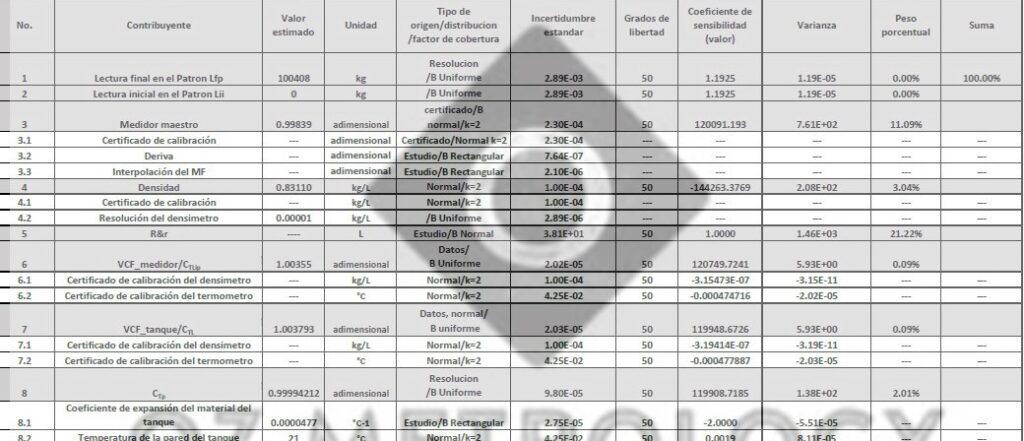
En las calibraciones en el día a día se ven estas fuentes de incertidumbre. En el caso del inciso f) se aprecia en la Figura 2 y 3 un ejemplo de fuente de incertidumbre, la resolución del instrumento bajo calibración o ensayo.

En algunos casos como en la Figura 3. se tienen dos fuentes de incertidumbre por el propio instrumento, una asociada a la lectura que aprecia el técnico y otra de la división de la escala del instrumento.

En el caso del inciso g) se trata del error y la incertidumbre asociada a la calibración del equipo patrón que se este utilizando. En el certificado de calibración, el metrologo debe corregir los valores de su patrón en toda la escala o rango del equipo. Se debe usar las curvas de regresion e interpolación que modelen adecuadamente el comportamiento del error y al incertidumbre del equipo.

Procedimiento de evaluación, tipos de incertidumbre y expresión de la incertidumbre

Modelo matématico

Lo primero que se establece es la relación funcional matemática entre la magnitud a medir (Y) y las magnitudes de entrada (X), dentro de las cuales se consideran las magnitudes influyentes. A esta relación funcional se le conoce como modelo matemático que viene dado de la forma Y=f(x₁,x₂,…, x_n). En la gran mayoria de los casos el modelo matemático es el error.

Por ejemplo en la ecuación 1 se muestra el modelo matemático del volumen a 20 °C por método gravimétrico. En la ecuación 2 el error de indicación de una balanza en la prueba de linealidad. Las correciones δ tienen valor cero como valor esperado pero sí las incertidumbres asociadas a cada una de ellas.

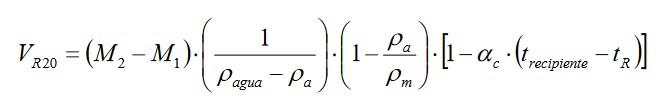
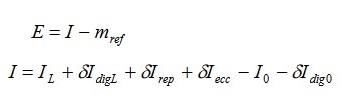
Tipos de incertidumbres

Lo segundo es estimar las incertidumbres de las magnitudes de entrada (x) empleando evaluaciones Tipo A y Tipo B.

Tipo A: Cuando la incertidumbre se evalúa a través del análisis estadístico de series de mediciones.

Tipo B: Cuando no se dispone de series de datos para evaluar la incertidumbre, pero existe un conocimiento a priori que permite conocer que tipo de distribución siguen los datos.

Una incertidumbre estándar de Tipo A puede obtenerse de cualquier método estadístico que ofrezca un estimado válido de la dispersión de los datos. En la mayoría de los casos, la mejor estimación disponible del valor esperado m_q  de una magnitud  q  que varia aleatoriamente y de la cual se han obtenido  n  observaciones independientes  q_k  bajo las mismas condiciones de medición, es la media aritmética o promedio  q  de las  n  observaciones.

Las observaciones individuales  q_k  definen el valor debido a efectos aleatorios. La varianza experimental de las observaciones  S²  (la cual estima la varianza   s²  de la distribución de probabilidad de  q ). La raíz cuadrada positiva de la varianza experimental es la denominada desviación estándar experimental, la cual caracteriza a la variabilidad de los valores observados  q_k , o más específicamente, su dispersión alrededor de la media  q. En la ecuación 3 se aprecia como se expresa la incertidumbre tipo A.

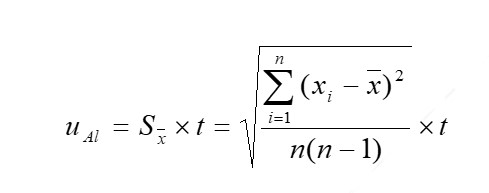
Para un estimado  x_i  de una magnitud  X_i  que no se obtuvo a partir de observaciones repetidas, la incertidumbre estándar  u (x_i )  es evaluada mediante juicios y criterios científicos basados en toda la información disponible sobre la variabilidad de  X_i.  Esta información puede incluir:

• Datos de mediciones anteriores;
• Experiencia o conocimiento general de las características y el comportamiento y las propiedades de los materiales e instrumentos;
• Especificaciones del fabricante;
• Datos obtenidos de los certificados de calibración u otras certificaciones;
• Incertidumbres asignadas a datos de referencia tomados de manuales u otras fuentes.

La información disponible para una evaluación Tipo B de la incertidumbre estándar requiere de una visión basada en la experiencia y el conocimiento general, y es una habilidad que puede aprenderse con la práctica. Debe reconocerse que una evaluación de incertidumbre estándar Tipo B puede ser tan confiable como una evaluación Tipo A.

Un ejemplo muy común de evaluación Tipo B es en el caso de instrumentos con indicación digital, la resolución de los mismos implica una incertidumbre en el resultado de la medición la cual será: u=0.29*Res, donde Res es la resolución del instrumento.

Incertidumbre estandar combinada

La incertidumbre  estándar  combinada  del resultado de una medición, denominada por  u_c (y), se considera que es el estimado de la desviación estándar del resultado y se obtiene a partir de la combinación de todas las incertidumbres ya sean de Tipo A  o  B. La combinación de todas las incertidumbres se efectúa aplicando la ley de propagación de la incertidumbre.

Hay dos casos, el primero que veremos es aquel  en que todos los argumentos son independientes, o sea no correlacionados, y el segundo es aquel en el que dos o más argumentos están correlacionados. En la ecuación 4 se muestra el caso cuando no hay correlación y en la ecuación 5 cuando existe este fenómeno.

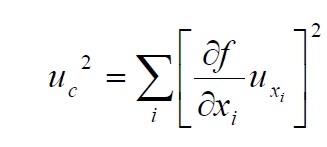
El término diferencial se conoce como coeficiente de sensibilidad y es el que relaciona las unidades de las magnitudes de entrada con las de salida. En la ecuación 1 se tiene como magnitud de salida el volumen. La unidad de volumen es el L, pero se tiene la masa del recipiente vacio M1 y la masa del recipiente lleno M2, los cuales se expresan en unidades de masa como mg, g o kg. Se deriva con respecto a la masa y se obtiene el coeficiente de sensibilidad de la masa, su dimensión será (L/g), por este motivo cada diferencial debe ser multiplicado por su incertidumbre típica.

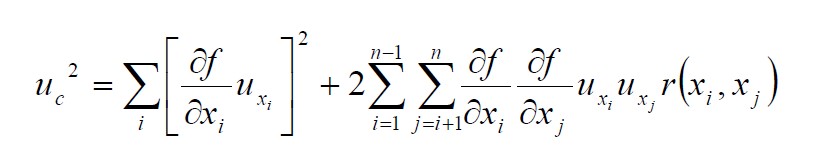
Incertidumbre expandida

Aunque la incertidumbre estándar combinada se puede utilizar para expresar la dispersión, es necesario ofrecer una medida de la incertidumbre que represente un intervalo alrededor del resultado de medición, dentro del cual se encuentren los valores que pueden ser atribuidos al mensurado con un determinado nivel de confianza.
El resultado de la medición se expresa por tanto de la forma Y = y ± U que se interpreta como que y es el mejor estimado del valor atribuible al mensurado Y. El intervalo definido por y – U ; y + U contiene a los valores que pueden atribuirse razonablemente a Y con un determinado nivel de confianza

Se denomina incertidumbre expandida U, a la que se obtiene de multiplicar la incertidumbre estándar combinada por un factor k llamado factor de cobertura, ver ecuación 6.

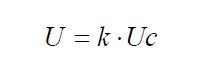
El factor de cobertura se selecciona sobre la base del nivel de confianza que se desea asociar al intervalo de confianza y – U ; y + U . En la calibración de los instrumentos de medición generalmente se recomienda el valor convencional k=2 que corresponde a un nivel de confianza aproximado del 95 % para una distribución normal. Estimar el factor de cobertura significa que cuan bien u_c (y) estima la variabilidad asociada al resultado de la medición. Para ello es necesario conocer la distribución de probabilidades que describe la magnitud de salida, aspecto de gran complejidad inclusive para pocas variables.

En la práctica se aplica el Teorema del Límite Central que establece que la distribución de los valores de la magnitud de salida puede ser considerada aproximadamente como una distribución normal si su varianza σ²(y) es mucho mayor que cualquiera de las contribuciones individuales c_i²σ²(x_i) de las magnitudes de entrada.

Una consecuencia práctica inmediata del Teorema del límite central es que cuando la incertidumbre combinada de un resultado de medición no está dominada por una de las componentes de incertidumbre de las magnitudes de entrada, en la incertidumbre expandida U_p=k_pU_c(y) que define un intervalo de confianza con un nivel de confianza P es asignar a k_p el valor que corresponde asumiendo una distribución normal. En la tabla 1. siguiente se dan valores de k para niveles de confianza típicos.

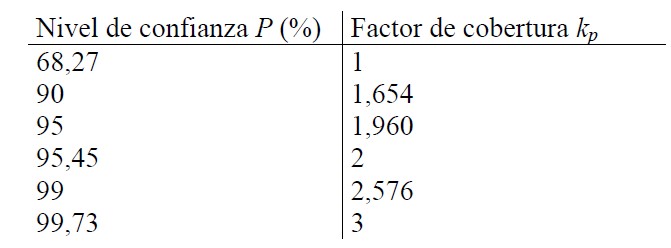
Para obtener una mejor aproximación en la definición de los intervalos de confianza en lugar de emplearse la distribución normal se requiere emplear la distribución de student y el factor de cobertura k_p entonces se determina a partir del coeficiente t de student evaluado en el número de grados de libertad efectivos del estimado de salida, o sea, k_p=t(υ_ef).

Grados de libertad efectivos

Lo anterior es una consecuencia de que para la incertidumbre estándar combinada u_c(y) la medida de la incertidumbre está en función del número de grados de libertad efectivos (υ_ef ) del estimado de salida y que en buena aproximación se obtiene combinando los grados de libertad de los estimados x_i de las X_i magnitudes de entrada. Esa combinación se obtiene a través de la llamada fórmula de Welch-Satterthwaite en la ecuación 7.

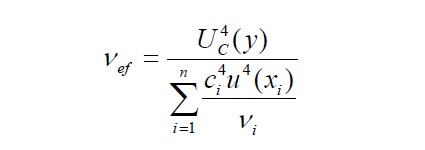
Expresión de la incertidumbre de medición

Como resultado de la calibración de un instrumento de medición la incertidumbre debe expresarse en el Certificado de Calibración de manera clara y sin ambigüedades. Como la incertidumbre es una medida de la calidad de la medición realizada por el proveedor del servicio y al mismo tiempo un elemento esencial en la trazabilidad de las mediciones que posteriormente realiza el usuario del instrumento, es necesario ofrecer la mayor cantidad de información acerca de cómo fue obtenida.

La información debe ser suministrada de tal forma que pueda ser interpretada de manera uniforme no sólo por el usuario del instrumento y los clientes de sus producciones o servicios, sino además por todos los interesados, entre ellos, los expertos y auditores de los organismos de Certificación y Acreditación.

Se establecen determinadas reglas para la expresión uniforme de la incertidumbre de los resultados en el presupuesto de incertidumbre, algunas de las cuales se presentan seguidamente:

• La incertidumbre no deben informarse con un número excesivo de dígitos. Es suficiente emplear dos cifras significativas, aunque en algunos casos se pueden ofrecer algunos dígitos adicionales para evitar redondeo.
• Dar el valor de cada estimado de entrada x_i, su incertidumbre U(x_i) e informar acerca de su distribución de probabilidades.
• Dar las covarianzas estimadas y los coeficientes de correlación para todas las magnitudes de entrada correlacionadas y el método de cálculo empleado.
• Dar los grados de libertad para la incertidumbre estándar de todos los estimados de entrada.
• Dar la relación funcional entre las magnitudes de entrada y salida y cuando se considere útil, los coeficientes de sensibilidad.

Mejor capacidad de medición (CMC)

La mejor capacidad de medición se define como la menor incertidumbre de medición que un laboratorio puede lograr al realizar calibraciones más o menos rutinarias de patrones o instrumentos casi ideales.

La expresión “más o menos rutinaria” se refiere a que el laboratorio debe ser capaz de lograr la incertidumbre declarada en el trabajo normal que realiza aunque en determinadas ocasiones el laboratorio obtenga mejores resultados como consecuencia de realizar un análisis extensivo o tomar precauciones extras, casos que no deben estar contenidos en la mejor capacidad de medición.

Por otra parte la frase “casi ideales” significa que la mejor capacidad de medición no debe depender de las características del calibrando. Resulta obvio que el calibrando contribuye a la incertidumbre, lo que se quiere transmitir es que tal contribución no sea significativa.

El laboratorio no debe presentar una incertidumbre menor a la mejor capacidad de medición para los servicios que tiene acreditados.

El término CMC comenzó a ser usado por laboratorios acreditados y órganos acreditadores refiriéndose a aquellas nomenclaturas dentro del alcance de acreditación, siendo uno de los parámetros que emplean tales órganos para establecer dicho alcance. Siendo así una de las informaciones esenciales que deben estar en los directorios de laboratorios acreditados ya que permite realizar un juicio sobre la capacidad de un laboratorio para realizar determinada calibración o medición.

La tabla CMC debe contener todas las componentes significativas de incertidumbre así como derivas temporales u otras variaciones que puedan afectar la estabilidad del resultado. Hay casos en los que la incertidumbre de medición depende de parámetros adicionales como pueden ser las condiciones ambientales o la frecuencia entre otros. En estos casos debe declararse el o los valores de tales parámetros para los que se reporta la mejor capacidad de medición.

Conclusión

Estimar la incertidumbre de la medición no es fácil. Requiere mucho tiempo y esfuerzo. Sin embargo, con los procesos, las fuentes de información y las herramientas adecuadas, el análisis de la incertidumbre no tiene por qué ser difícil.

En esta guía, he presentado los principales pasos para ayudarlo a calcular la incertidumbre de la medición. Si bien esta no es una guía práctica completa, le he brindado mucha información para ayudarlo a realizar la estimación de la incertidumbre usted mismo.

Entonces, comience a estimar la incertidumbre y dígame qué funciona para usted. Si tiene preguntas o sugerencias adicionales que ayudarán a mejorar esta guía, comuníquese conmigo y comparta sus comentarios. Estaré encantado de recibir sus comentarios.

Referencias

JCGM/WG1. (2008). JCGM 100:2008 – Evaluation of measurement data – Guide to the expression of uncertainty in measurement. Sèvres: BIPM.

United Kingdom Accreditation Service. (2012). M3003: The Expression of Uncertainty and Confidence in Measurement. Middlesex: United Kingdom Accreditation Service.

Traceable Temperatures: An Introduction to Temperature Measurement and Calibration, 2nd edition By J.V. Nicholas and D.R. White, Wiley Publishers, 2002.